做了一道数学几何题
John Hattie的visible learning，这本书集成了两亿多学生的数据，然后得到了哪些品质能够决定一个人学习好坏，想通过一道几何题目来验证下。先看下John Hattie的结论
哪些品质能够决定一个人学习好坏
排在第一名的品质是复盘、总结能力
简单的说，这个能力就是这个孩子心里是否有个“小教练”，能够每次跳脱出当前任务，帮助自己分析，失败在哪里，成功在哪里，如何进阶，如何训练等等。
举几个例子：
如果写不出作文，这个“小教练”能告诉孩子，是没有素材，还是文字能力不强。
如果是文字能力不强，应该如何训练（是造句，还是拆段落）
如果数学题做不出来，这个“小教练”能告诉孩子，我的弱点在哪里，哪个类型题我有重大问题，是因为哪里没有理解和打通。
有内化的“自我教练”，这个能力系数是1.67。也就是其他能力相当，学习效果可以翻1.67倍。
排在第二名的是建构能力。简单的说是逻辑推理，做事顺序等等
在内心“小教练”能把问题进行拆解之后，建构能力能把这些问题进行排序，应该怎么做更合理。
最终怎么把训练步骤整合。遇见一个问题，先干什么，再干什么等等。
有很强的顺序能力，系数为1.44。也就是其他能力相当，学习效果可以翻1.44倍。
排在第三名的能力是智商和过去成绩
这个毋庸置疑，聪明做事就会简单一些。平均效应系数为0.67。
也就是说，其他能力相当，智商高和过去成绩好，学习效果提升67%
智商重要程度应该比这里更高，但是实际高智商的太少，大多都是因为基础知识好给人产生了智商高的误解！
排在第四名的能力是自我驱动力
简单的说，知道自己为什么学习，能够自我鼓励，遇见失败能抗挫，有很强的心理驱动力。
平均效应系数为0.48。也就是说，其他能力相当，有自我驱动力的人，学习效果提升48%。
排在第五名的才是集中注意力
也就是说，注意力强。注意力对学习影响，并没有很多家长想象的那么大。
注意力的平均效应系数为0.44
也就是说，其他能力相当，注意力好的孩子，效果能提升44%
———总结一下——-
学习提升的个人因素：
自我分析，自我教练的元认知能力 》 逻辑排序与制定计划的建构能力》 智商和过去成绩 》自我驱动力》 集中注意力。
很多家长痴迷于“专注力”。当然专注力是一个效应量很强的学习力，但是从整体数据看，对学习的提升效果，仅仅排到第五名。
帮助孩子建立元认知能力和建构能力的培训，才能给他们对终身学习有帮助的技能包
以上缺少了对方法的落地执行能力的评估，实际这是影响最大的
案例数学几何题
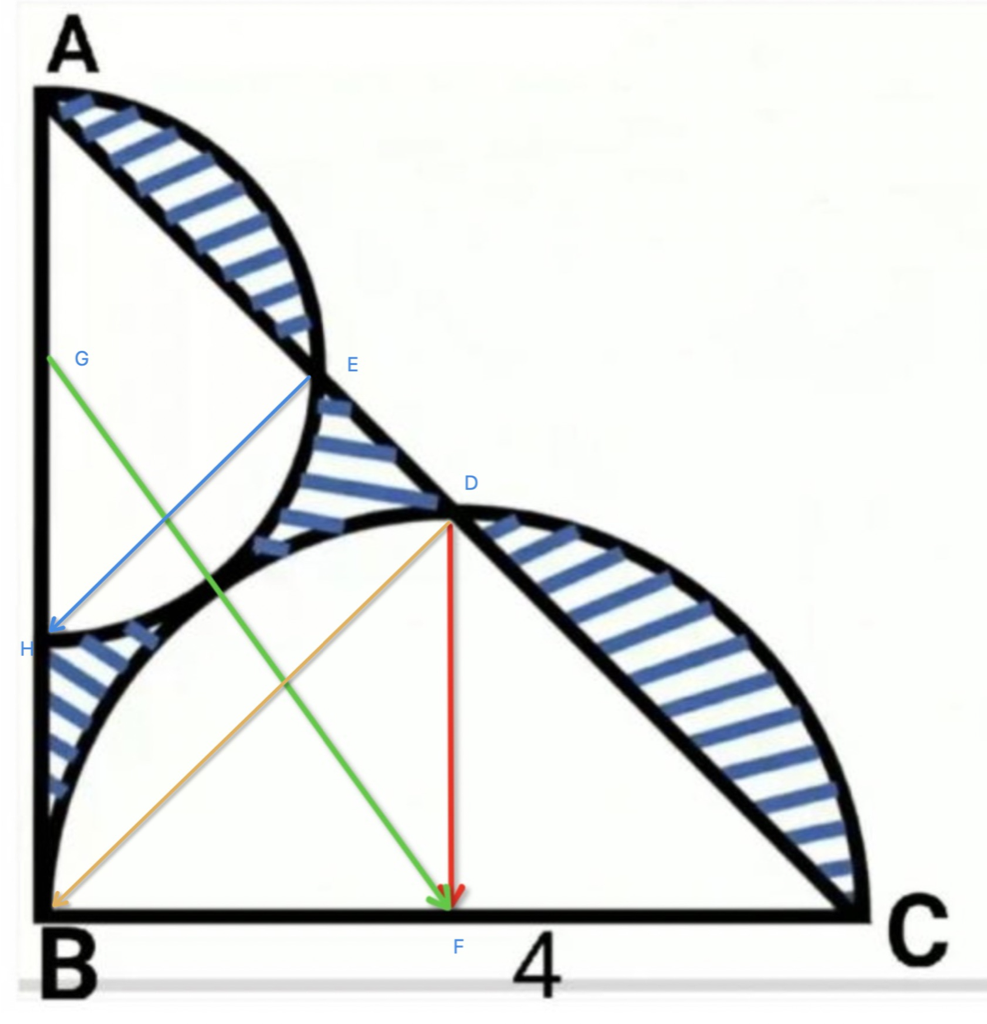
题目如下（图中红色、绿色线是我绘上去的辅助线）
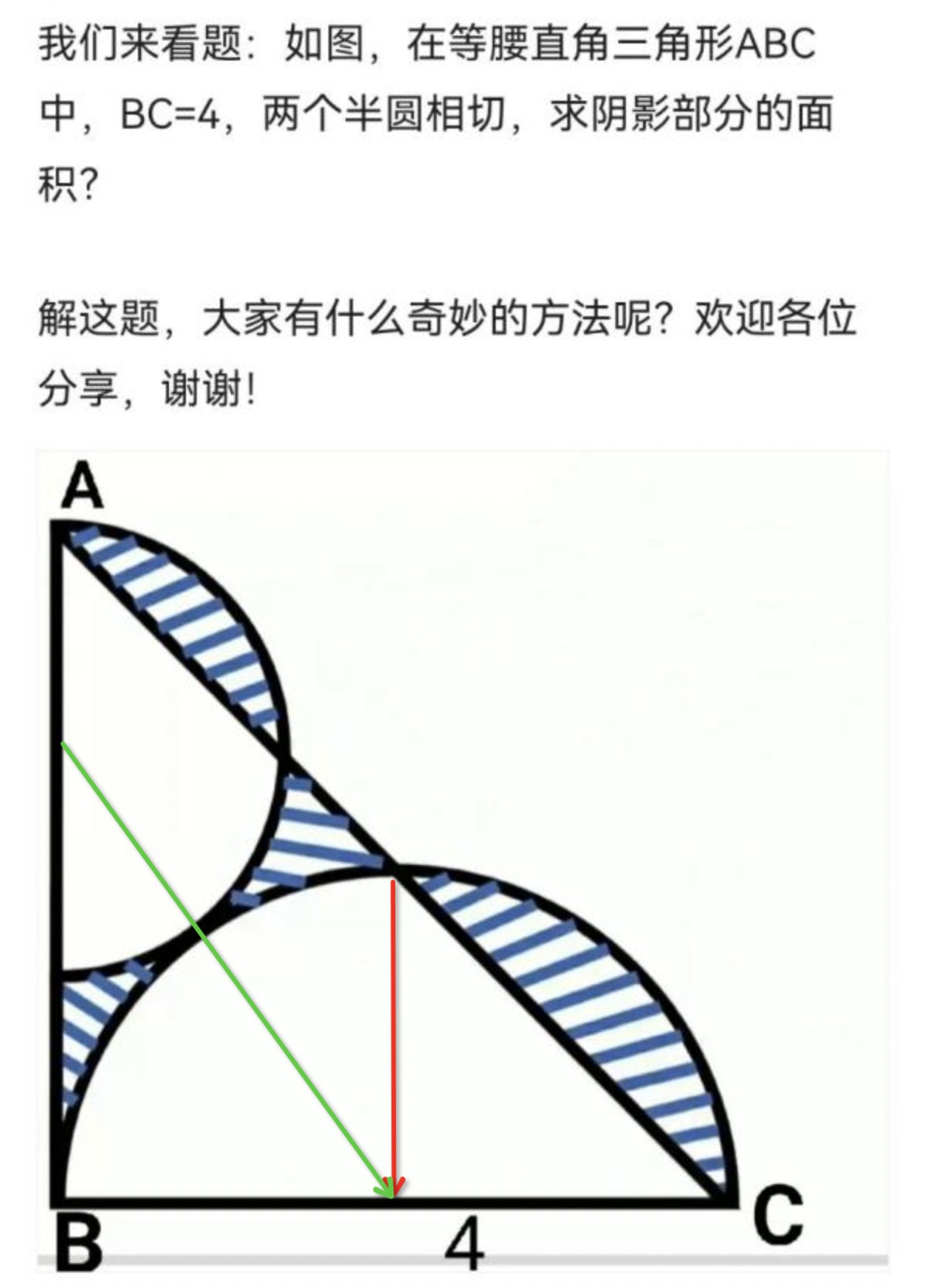
目标分解
求得四个阴影部分的面积相加；
求得白色部分面积即可以得到三角形内部两块阴影部分面积；
求得红色三角形面积记得通过圆面积减得三角形面积得到三角形外部阴影面积。红色辅助线、绿色辅助线
题目给出的条件
大三角形是等腰直角三角形（两个角都是45度，直角90度）；
两圆相切：圆心连线经过切点，连线长度为两圆半径相加。大圆半径为2
这里关于两圆相切我完全不记得有啥特性了，所以去Google了一把得到如下两圆相切的特性：
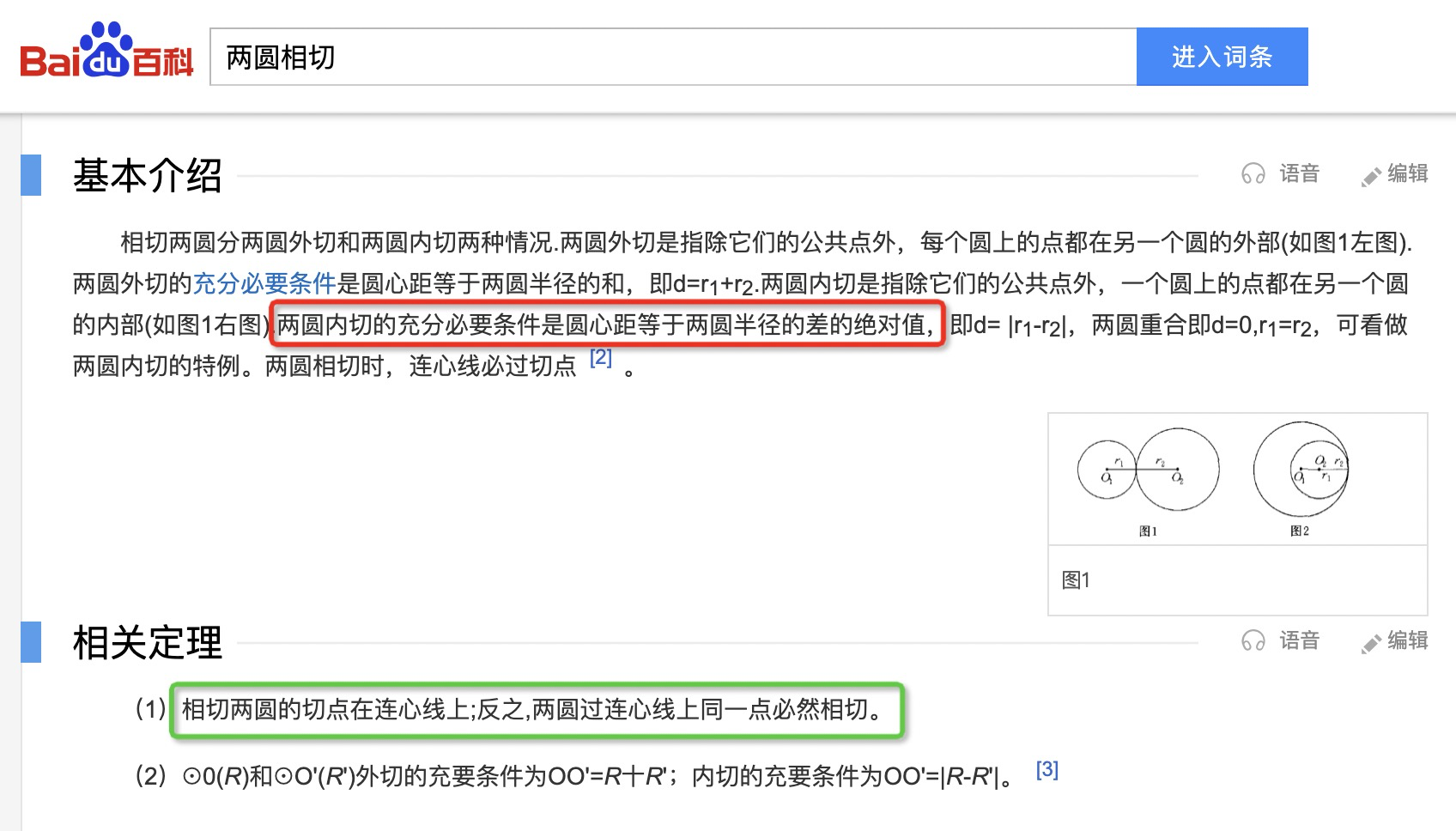
想了一下在我丢开课本几十年后我看到等要直接三角形我能得到：45度、两条边相等这两个结论；但是看到两圆相切我完全想不起来这是什么东西了。相信这两个知识点在我中学的时候肯定无比熟练。
但是两圆相切完全不会出现在我的生活和应用中，但是等要直接三角形太常见了，它反复出现在我的生活中，所以我只要没得老年痴呆应该会一直记得。
解题关键
- 如何求得小圆半径；
- 如何求红色辅助线构成的右下角三角形的面积（是否是个等腰直角三角形？），求得这个三角形的面积就能算出右下角阴影面积
- 从1的小圆半径和2的方法同理可得左上角的外部阴影面积
- 从2、3的阴影面积可以求得大三角形内部两块白色区域面积
- 这样的到了全部阴影的面积
详细步骤
- 求解小圆半径：相切是切入点，两圆圆心连线经过想切点（连线长=大圆半径+小圆半径）（绿线）
- 利用等腰直接三角形得到左下角绿色新直角三角形由勾股定理算出小圆半径（绿线）
- 大圆交点到圆心作辅助线得到右下角等腰三角形，由一个角是45度，和等腰三角形的特点退出另外一个角也为45度，从而得到右下角红色三角形是等腰直角三角形（红线）
- 通过大圆四分之一面积减掉右下角红线等腰三角形面积得到右下阴影部分面积，同理可得右上阴影面积。
- 通过半圆面积减掉阴影面积可分别得到两个半圆内部的白色部分面积
- 大三角形面积减掉6中的两个白色面积得到两个小阴影面积
- 到此分别得到了四个阴影部分面积
大圆半径很容易求得为2，设小圆半径为r，根据左下角绿色直角三角形的勾股定理有：(4-r)(4-4)+2X2=(2+r)(2+r)，可得r=4/3
右下角的红色三角形是个等腰三角形，且一个底角为45度，可得这个三角形是等腰直角三角形，求得大圆半径为2
复盘求解过程
教练在哪里?
教练就是日益自我训练的过程，教练在事后复盘上述过程，解题过程中没有教练参与
如果做不出来，那么教练就来问：
是题目没读懂得到的信息不够（仔细多读题，提高阅读能力）；
还是由题目中的已知条件得不到相关的直接推理（比如两圆相切因为不了解特性，所以得不到连线就是两个圆半径之和—-这种只能多看书）；
或者推不出来右下角的直角等腰三角形（对等腰三角形理解不够）……
如果做得过于绕，那么教练就来问：
还能简化（这个简化不是要奇技淫巧的快解），而是要既解决问题又不啰嗦，同时又是自己掌握知识的恰切运用！
教练就是复盘上述过程，得到方法进步或者知识缺陷或者理解缺陷，而不是得到答案。
逻辑推理，做事顺序
先求什么再求什么，怎么样从已知条件得到简单结论，然后再分步得到阶段性小结论（各个小块面积）到最终目标，这就是John Hattie提到的逻辑推理做事顺序能力
基础知识的运用
勾股定理、等腰三角形、三角形三角之和、相切特性、圆面积、等腰三角形面积计算
没有任何一个复杂的基础知识，也没有任何需要几次的推导，全是定理带来的直接特性，对智力要求极低
自我驱动和集中注意力是个长期过程，自我驱动决定了之前的学习欲望和基本知识点的掌握
其他总结
你有更巧妙的解法？对不起，我不需要，我要的就是这种学渣也完全能掌握，只需要简单地1+1+1+1就得到4的方法，我不需要2*2得到4，因为1+1+1+1对不会乘法的学渣也能掌握，我要的就是这种普适的方法。
学渣也能掌握这个方法，然后用这个方法训练自己解决其他类似题目。对学渣来说考80分就很开心了，等他们有了考80分的能力就有野心向90进发。
学渣更重要的是追求容易的全部解决，复杂的直接战略性放弃，只有在容易的全部掌握后才能慢慢挑战复杂题目。容易的基础题都解决不好只是追求奇技淫巧的解法或者复杂题目容易迷失自己和快速遗忘。
受过训练的中学生如何解这题
做如下BD和HE两条辅助线，梯形BDEH的面积就是要求的面积。
也就是ABC三角形的面积减掉AEH和BCD两个三角形的面积。
那么需要证明 BD=CD，因为DF=CF，角FCD为45度，所以CDF为等腰三角形，接下来证明过程和上面一样。同时同理可证AEH也是等腰直角三角形。
可以看到受过训练的中学生的解题方法更为犀利一些，但是前面文章的方法最为朴素和直接。训练过的方法效率更高，当然两个方法基本知识的运用没有差别。
比如受过训练的方法还是需要下图红色、绿色两条辅助线。这就是职业和业余的差距。
最后如果你发现我题目做错了，也别较真了，我就是借案例说明下学习方法，不代表我现在还有初中数学能力